This tutorial series begin where Part 1 left off. In this second tutorial, we’ll explain the second category of search algorithm Heuristic searches that were introduced in the previous tutorial. The code for this program can be found in my github account, the link being here:- https://github.com/aelhirach/AIAlgorithms.

Heuristic searches

Unlike a blind search, an heuristic search is a search that uses a method (usually called an heuristic function) or set of rules to search a solution space based on some relevant additional information about states. This method or rule set must be applied repeatedly in order to eventually satisfy some goal condition which indicates that a solution has been found.

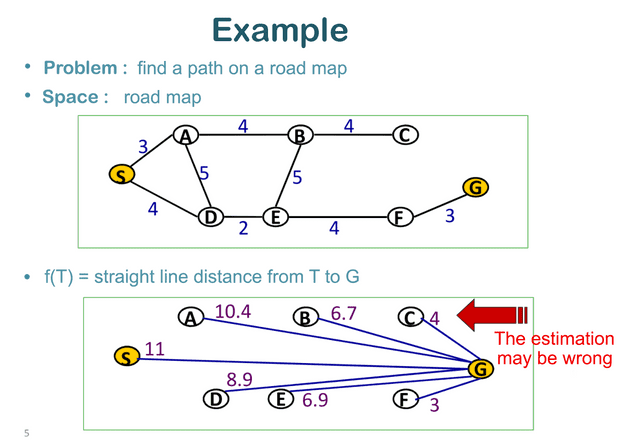
The principle of a heuristic can be applied to various problems in mathematics, science and optimsation in order to find approximate (still not optimal) solutions quickly. The use of heuristic search algorithms has expanded considerably to include a variety of applications, such as route planning, computational biology and robotics. The following figure illustrates how the heuristic solves a road map problem :

There are many heuristic search algorithms, the following are some examples I came across (there might be others) :

• Hill climbing
• Beam search
• Hill climbing 2
• Greedy search

In this tutorial we are going to explain only two of them : Beam search & Greedy search

Beam search

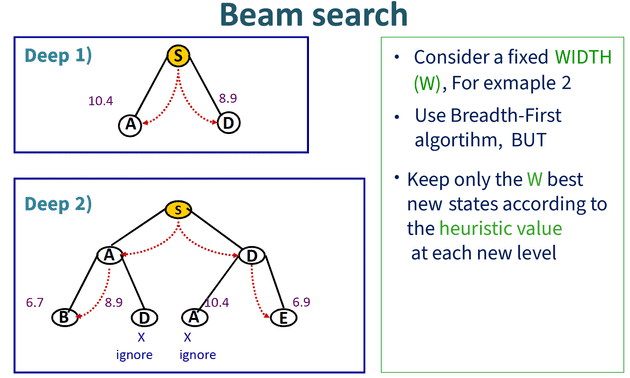
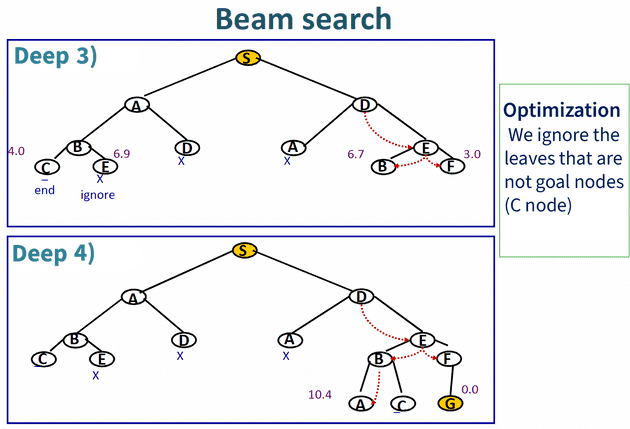
Beam search is an optimization of the breadth-first algorithm (BFS) we have seen in the first tutorial. It generates all the children of the current level’s state at each level of the tree and then orders them according to some heuristic. However, it only stores W (Width) number of the best nodes at each level called the beamwidth. Only those nodes are kept as successors.

Another optimization for Beam search algorithm is to ignore the leaves that are not goal nodes.

Greedy search

Breadth-first search traverses the tree level by level, visiting all of the nodes on the top level first, then all the nodes on the second level, and so on.

Beam search algorithm

The C# code of BeamSearch algorithm is a bit different from the previous blind search algorithms (BFS and DFS). Indeed, at each loop, it is necessary to store all the children of the same depth and then take only the n-best nodes according to the heuristic (n is the path width). Therefore, this function takes another parameter which corresponds to the value of the path width. To implement this algorithm, we will use 4 lists :

• List 1 : is the main queue that contains the paths, at each loop will be emptied and copied into the list 2.
• List 2 : is a temporary list that contains at each loop all the nodes of list 1. Thus, we can browse this list and generate all the children without loop in a list 3.
• List 3 : this list will contain the children (without loop) of the nodes in list 4.
• List 4 : this list is used to optimize the algorithm by eliminating the leaves that are not gaol.

The last step is to sort the list 4 according to the heuristic value and take the n-best children.

 // BeamSearch Algorithm

 public List<Path> BeamSearch(Node root, int width) {
            if (root == null) return null;
            bool isGaol = false;
            var queue = new List<Path>();
            root.state = VisitState.Visited;
            queue.Add(new Path(root));
            while (queue.Any() && !isGaol)
            {  //remove all paths from the QUEUE
                var tempQueue = new List<Path>();
                foreach (Path path in queue)
                    tempQueue.Add(path);
                queue.Clear();
                // create new paths (to all children)
                var childrenPaths = new List<Path>();
                foreach (Path p in tempQueue)
                {   
                   foreach (NodeCostPair child in p.Nodes.Last().Children)
                    {
                        //reject the new paths with loops
                        if (!p.Name.Contains(child.node.Name))
                        {   
                            Path childPath = new Path();
                            childPath.Nodes.AddRange(p.Nodes);
                            childPath.Nodes.Add(child.node);
                            childrenPaths.Add(childPath);
                            if (child.node.Name == "G")
                            {
                                isGaol = true;
                                goto Finish;
                            }
                        }
                    }
                }
                //Optimization : “remove the paths with no successors”
                for (int i = childrenPaths.Count - 1; i >= 0; i--) {
                     var childWithoutLoop = new List<NodeCostPair>();
                     for (int j = 0; j < childrenPaths[i].Nodes.Last().Children.Length; j++)
                     {
                         if (childrenPaths[i].Nodes.Last().Children[j].node == null) break;
                         else if (!childrenPaths[i].Name.Contains(childrenPaths[i].Nodes.Last().Children[j].node.Name))
                             childWithoutLoop.Add(childrenPaths[i].Nodes.Last().Children[j]);
                     }
                     if (childWithoutLoop.Count == 0)
                         childrenPaths.Remove(childrenPaths[i]);  
                }
                //take only width paths
                Finish: ;
                  childrenPaths = childrenPaths.OrderBy(o => o.Heuristic).ToList();
                  queue = childrenPaths.Take(width).ToList();       
                }
                return queue;
    }

Greedy search algorithm

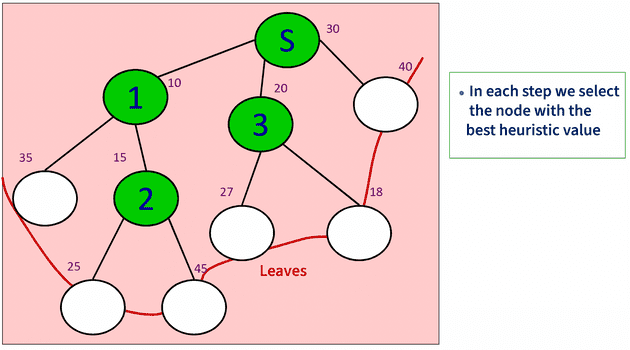
The GreedySearch algorithm consists in selecting at each step the node with the best heuristic value. For this, we will use two lists in the code :

List 1 : this is the main queue containing the paths, at each loop we delete only the first path.

List 2 : this is a temporary list that will contain the children without loop of the first path.

Then we add all the children nodes of the list 2 to the list 1 and we sort it according to the heuristic value.

At the end of the algorithm, the GreedySearch method sends a list of the paths traveled as well as the path leading to the goal.

  // GreedySearch Algorithm
  public List<Path> GreedySearch(Node root)
        {
            if (root == null) return null;
            bool isGaol = false;
            //queue des chemins
            var queue = new List<Path>();
            root.state = VisitState.Visited;
            queue.Add(new Path(root));

            while (queue.Any() && !isGaol)
            {
                Path p = queue.First();
                queue.RemoveAt(0);
                List<Path> tempList = new List<Path>();
                foreach (NodeCostPair child in p.Nodes.Last().Children)
                {
                    if (!p.Name.Contains(child.node.Name))
                    {   //[SA|SD]
                        Path childPath = new Path();
                        childPath.Nodes.AddRange(p.Nodes);
                        childPath.Nodes.Add(child.node);
                        tempList.Add(childPath);
                        //[(A)|(S)]
                        if (child.node.Name == "G")
                        {
                            isGaol = true;
                            goto Finish;
                        }

                    }
                }
                Finish:;
                queue.AddRange(tempList);
                queue = queue.OrderBy(o => o.Heuristic).ToList();
                        //[(A)|(S)]     
            }

            return queue;

        }

Conclusion

Unlike the blind searches, heuristic searches evaluate the available information (heuristic value) and makes a decision on which branch to follow. Heuristic algorithms reduce also memory usage and decrease the time complexity of problems by giving quick solutions (still not optimal). They are utilized in problems where additional information is available to determine the next step towards finding the solution. In the next tutorial we will learn the extended heuristic search algorithms using the Branch & Bround technique to find the optimal solution for general optimization problems.