Search Algorithms in AI : part 1 Blind Searches
Published on February 03, 2022

In this tutorial series we are going to learn a branch of Artificial Intelligence called search algorithms. There are too many search algorithms out there to fit in one tutorial. Therefore, this tutorial series will instead discuss five of the fundamental search algorithms, divided into the following tree categories :
- Blind searches : Depth First Search (DFS) & Breath First Search (BFS)
- Heuristic searches : BeamSearch & GreedySearch
- Optimal searches : Branch and bound (BB)
In the first tutorial we are going to explain two fundamental Blind searches Depth First Search (DFS) & Breath First Search (BFS). In the next tutorials, we will learn the two other categories of search algorithms, namely Heuristic & Optimal searches. A the end of this tutorial series, we will solve a maze game (labyrinth) with all those search algorithms. The code for this program can be found in its entirety in my github account, the link being here:- https://github.com/aelhirach/AIAlgorithms.
What is Artificial Intelligence & Search algorithms
In short, Artificial intelligence (AI) is a branch of computer science concerned with building agents that perform tasks requiring human intelligence. Mostly, these agents perform certain search algorithms in the background in order to achieve their tasks. To solve a search problem we need to ask the following questions :
1. Solution search :
- How to formulate the problem in a proper way ?
- How to find a proper solution ?
- How to find the best solution ?
2. Representation and structure of search spaces :
- How can we effectively represent the search space ?
3. Machine learning :
- How to implement algorithms that automatically improve (learn) by experience ?
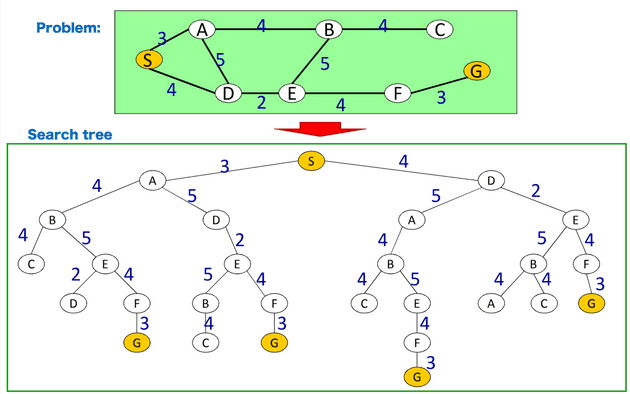
A search problem consists of a search space, an initial state, and a single or a set of goal states. A search space is a mathematical abstraction which can be represented in form of a graph or tree :
- the root represents initial state
- nodes represent states of the problem
- edges represent moves from a one state to another
- leaves represent final states.
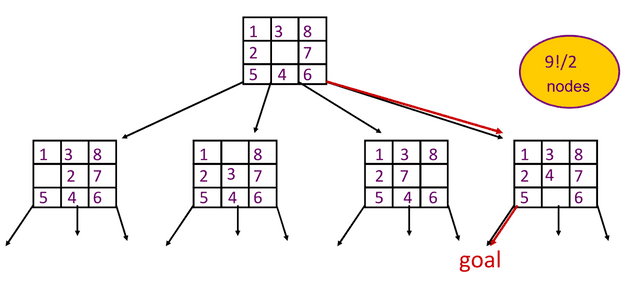
For example, in the 8-Puzzle game
- nodes: the different permutations of the tiles.
- edges: moving the blank tile up, down, right or left.
- The size of a search space : 9!/2
Many problems in computer science can be represented in form of graphs. For instance, mapping routes, network routing, and scheduling are graph problems. Search algorithms solve graph problems by going through the search space of the problem domain, they analyze or calculate the information stored within it, with either discrete or continuous values.
Blind searches
A blind search (also called an uninformed search) is a search that works with no information about its search space. The only thing that it can do is distinguish the goal state from all the others. There are many blind search algorithms. In this tutorial we are going to explain only two : Depth First Search (DFS) and Breath First Search.
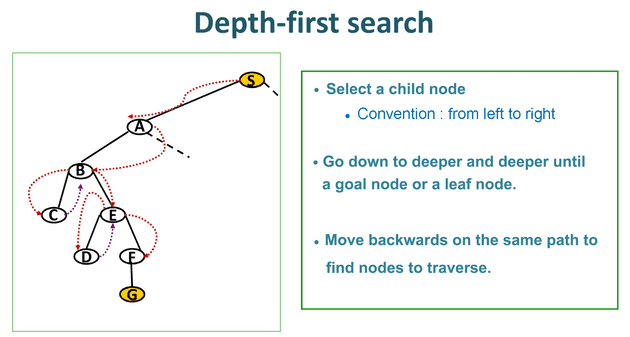
Depth-first search
Depth-first search traverses the tree branch by branch, it starts at the root node and goes as far as it can down to the leaf nodes at the bottom of the tree before trying the next branch over. The following figure illustrates how the DFS algorithm explores the tree step by step :
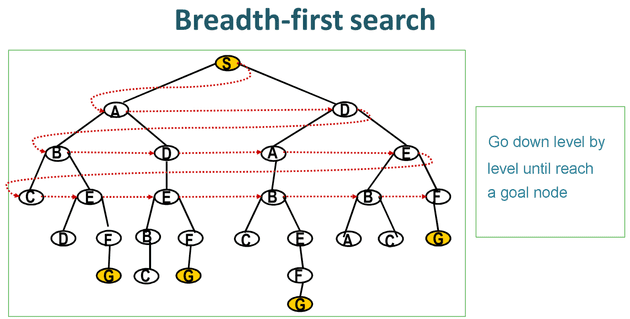
Breadth-first search
Breadth-first search traverses the tree level by level, visiting all of the nodes on the top level first, then all the nodes on the second level, and so on.
Programming search algorithms with C# language
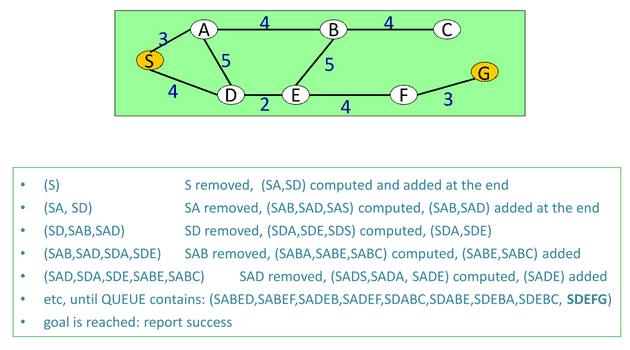
Let’s put all these things into practice with C# language. Firstly, we are going to define some common concepts and vocabularies between all the search algorithms. It is to be noted that we have not discussed some of them yet, so don’t be afraid if you don’t understand any vocabulary, we will explain it later when it’s necessary.
- Queue : a data structure which stores the crossed paths with the search algorithm
- Graph : a hierarchical structure consisting of several nodes
- Node : an element in a the graph
- Path : a set of successive nodes
- VisiteState : represents the state of a node (Unvisited, Visiting or Visited)
In order to model these different objects in object-oriented programming, we will create for each a particular class or struct :
-
<Graph> Class : the methods and variables of the Graph class are :
- count : an integer variable representing the number of nodes in the graph.
- addNode(Node n) : we use it to add nodes to the graph.
- getRoot() : as its name suggests, it allows to get the root node of the graph.
- getGoal() : it returns a goal node in the graph.
class Graph
{
// attributs
public int _count; // num of _vertices
private Node[] _vertices;
// Properties
public Node[] Vertices
{
get { return _vertices; }
set { _vertices = value; }
}
// Constructors
public Graph(int graph_Length)
{
_vertices = new Node[graph_Length];
_count = 0;
}
// Methods
public void addNode(Node n)
{
if(_count < _vertices.Length)
{
_vertices[_count] = n;
_count++;
}
else
{
Console.WriteLine("graph full");
}
}
public Node getGoal()
{
Node goal = null;
foreach (Node n in this.Vertices)
if (n.IsGoal){
goal = n;
break;
}
return goal;
}
public Node getRoot()
{
Node root = null;
foreach (Node n in this.Vertices)
if (n.IsRoot)
{
root = n;
break;
}
return root;
}
}-
<VisitState> enum : an enumeration defining a list of node states.
public enum VisitState { Unvisited, Visiting, Visited };
-
<NodeCostPair> struct : it contains a pair of variables : the parent node and the cost from the parent node. It allows for each node to be associated to its parent with a given cost”.
public struct NodeCostPair { public Node node; public double costToParent; }
-
<Node> class : the methods and variables of the Graph class are :
- isRoot, isGoal, isTrap : flags representing the type of the node.
- Children : an array of NodeCostPair holding children associated to the current node with a given cost.
- ChildrenCount : represents the number of the children of the current node.
- HeuristicValue : we will need this value in the heuristic searches : BeamSearch & GreedySearch.
public class Node
{
// attributs
private NodeCostPair[] _children;
private int _childrenCount;
private String _name;
private bool _isRoot = false;
private bool _isGoal = false;
private bool _isTrap = false;
private VisitState _state;
private double _heuristicValue;
// Properties
public bool IsRoot
{
get { return _isRoot; }
set { _isRoot = value; }
}
public bool IsGoal
{
get { return _isGoal; }
set { _isGoal = value; }
}
public bool IsTrap
{
get { return _isTrap; }
set { _isTrap = value; }
}
public double HeuristicValue
{
get { return _heuristicValue; }
set { _heuristicValue = value; }
}
public NodeCostPair[] Children
{
get { return _children; }
set { _children = value; }
}
public VisitState State
{
get { return _state; }
set { _state = value; }
}
public String Name
{
get { return _name; }
set { _name = value; }
}
public String ChildCount
{
get { return _childrenCount; }
set { _childrenCount = value; }
}
// Constructors
public Node(String name)
{
this._name = name;
}
public Node(String name, int children_Length)
{
this.name = name;
_childrenCount = 0;
_children = new NodeCostPair[children_Length];
}
public Node(String name, int children_Length, double heuristic)
{
this._name = name;
this._heuristicValue = heuristic;
_childrenCount = 0;
_children = new NodeCostPair[children_Length];
}
// Methods
public void addChildNode(Node childNode)
{
childNode.State = VisitState.Unvisited;
if (_childrenCount <= _children.Length)
{
var child = new NodeCostPair();
child.node = childNode;
this._children[_childrenCount] = child;
_childrenCount++;
}
}
}-
<Path> class : the methods and variables of the Graph class are :
- Name : concatenation of node names
- AccumulatedCost : the accumulated from the root node to the last node in the path.
- getRoot() : as its name suggests, it allows to get the root node of the graph.
- HeuristicValue : we will need this value in the heuristic searches : BeamSearch & GreedySearch.
class Path
{
// attributs
private string _name;
private double _heuristic;
private double _estimatedCost;
private double _accumulatedCost;
private List<Node> _nodes;
/// Constructors
public Path(Node root)
{
_nodes = new List<Node>();
_nodes.Add(root);
}
public Path()
{
_nodes = new List<Node>();
}
///Proprieties
public List<Node> Nodes
{
get
{return _nodes;}
set
{ _nodes = value; }
}
public String Name
{
get
{
_name = string.Join("", _nodes.Select(node => node.Name));
return _name;
}
set
{
_name = value;
}
}
public double AccumulatedCost
{
get
{
_accumulatedCost = 0;
for (int i = 1; i < Nodes.Count; i++)
for (int j = 0; j < Nodes.ElementAt(i - 1).Children.Length; j++)
if (Nodes.ElementAt(i).Name == Nodes.ElementAt(i - 1).Children[j].node.Name)
{
_accumulatedCost += Nodes.ElementAt(i - 1).Children[j].costToParent;
break;
}
return _accumulatedCost;
}
set
{
_accumulatedCost = value;
}
}
public double Heuristic
{
get
{
_heuristic = _nodes.Last().HeuristicValue;
return _heuristic;
}
set
{
_heuristic = value;
}
}
public double EstimatedCost
{
get
{
return this._heuristic + this.__accumulatedCost;
}
set
{
_estimatedCost = value;
}
}
}Depth-first search algorithm
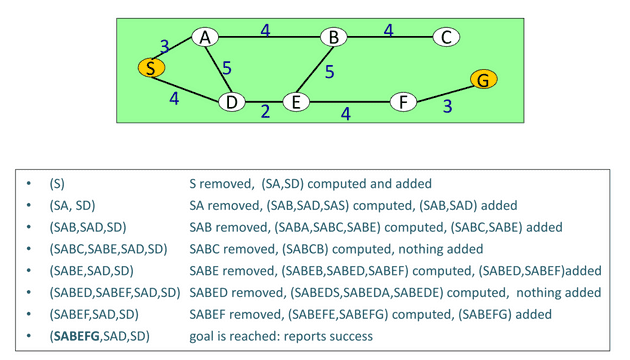
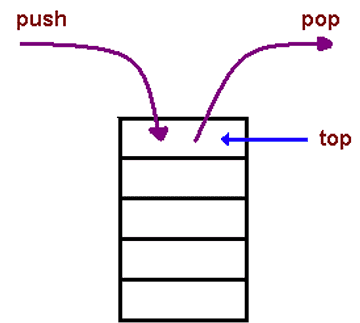
Since the DFS algorithm adds in each loop the children at the beginning of the Queue, we are going to create a method that returns a generic collection called Stack
// DFS Algorithm
public Stack<Path> Dfs(Node root)
{
if (root == null) return null;
bool isGaol = false;
//path queue
var queue = new Stack<Path>();
root.State = VisitState.Visited;
queue.Push(new Path(root));
while (queue.Any() && !isGaol)
{
Path p = queue.Pop();
foreach (NodeCostPair child in p.Nodes.Last().Children)
{
if (!p.Name.Contains(child.node.Name))
{
Path childPath = new Path();
childPath.Nodes.AddRange(p.Nodes);
childPath.Nodes.Add(child.node);
queue.Push(childPath);
if (child.node.Name == "G")
{
isGaol = true;
break;
}
}
}
}
return queue;
}Breadth-first search algorithm
Unlike DFS, BFS algorithm adds in each loop the children at the end of the Queue. This time, we are going to create a method that returns a generic collection diffrent from DFS called Queue
// BFS Algorithm
public Queue<Path> Bfs(Node root)
{
if (root == null) return null;
bool isGaol = false;
var queue = new Queue<Path>();
root.State = VisitState.Visited;
queue.Enqueue(new Path(root));
while (queue.Any() && !isGaol)
{
Path p = queue.Dequeue();
foreach (NodeCostPair child in p.Nodes.Last().Children)
{
if(!p.Name.Contains(child.node.Name)){
Path childPath = new Path();
childPath.Nodes.AddRange(p.Nodes);
childPath.Nodes.Add(child.node);
queue.Enqueue(childPath);
if (child.node.Name == "G"){
isGaol = true;
break;
}
}
}
}
return queue;
}Conclusion
In summary, a blind search is very flexible because it’s blind to the problem it’s trying to solve, we might just be looking for a solution and won’t know we’ve found it until we see it. That’s why it’s very useful when we don’t have any information about the search problem. However, this kind of algorithms doesn’t show to be intelligent enough to solve complex search problems, it doesn’t know anything special about the domain it’s working in and so often makes mistakes. In the next tutorials we shall learn the two other categories of search algorithms that have information on the goal state which helps in more efficient searching.
If you like it, share it!