Build a Pente game with Minimax algorithm and Alpha Beta Optimization on C#

Published on February 14, 2024

Introduction :

In the realm of Artificial Intelligence, the journey from basic search algorithms to more sophisticated strategies marks a profound evolution. Having explored fundamental search algorithms like Blind and Heuristic searches in previous tutorials, we now embark on a new frontier: game-playing algorithms.

Building upon the foundational knowledge laid out in the previous articles, we delve into the practical application of Minimax with Alpha-Beta pruning in the building of a Pente game with AI. While Blind and Heuristic searches provided valuable insights into problem-solving methodologies, Minimax with Alpha-Beta pruning introduces a paradigm shift in tackling strategic decision-making within game environments.

In this article, we transition from theoretical discussions to hands-on implementation, leveraging the power of Minimax with Alpha-Beta pruning to create a formidable digital opponent in the game of Pente. Through this journey, we not only deepen our understanding of AI algorithms but also witness their tangible impact on enhancing gaming experiences.

I have added this project on GitHub. Feel free to download and experiment with it! To make this project work, you need the following tools :

Visual Studio Code
C# Dev Kit extension
For .NET Development, the .NET SDK

1 - Why new techniques and algorithms for games? :

Game algorithms is a special case of a search problem, with some new requirements. They differ from basic search methods due to the inherent unpredictability of game environments, where opponent moves are unknown and constantly changing. Unlike traditional search problems with well-defined states and actions, games introduce uncertainty and dynamic decision-making, making it challenging to anticipate the opponent’s next move. This unpredictability significantly expands the search space, as each possible move by the opponent creates branching paths that need to be explored.

Basic search methods may struggle to handle this complexity efficiently, leading to impractical computational requirements. In contrast, game algorithms like Minimax with Alpha-Beta pruning are specifically designed to navigate these intricate search spaces, making informed decisions even in the face of uncertainty. By considering potential opponent moves and minimizing the search space through pruning techniques, game algorithms excel at adapting to dynamic game environments and crafting intelligent gameplay strategies.

2 - Minimax Game algorithm :

Minimax is a decision-making algorithm commonly used in two-player, zero-sum games, such as chess, tic-tac-toe, or Pente. The primary objective of Minimax is to determine the best move for a player by considering the possible moves of both players and choosing the one that maximizes the player’s chances of winning while minimizing the opponent’s chances.

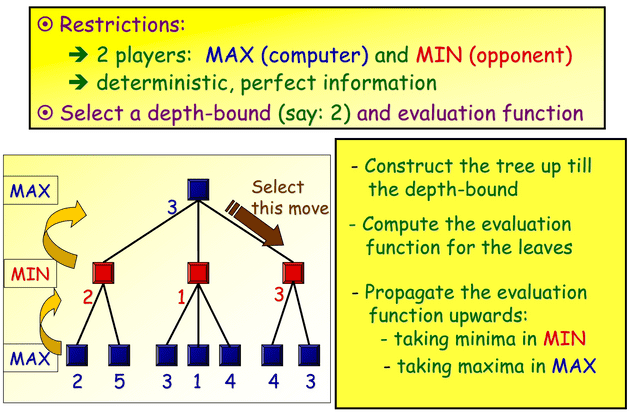
Step 1 : The first step in the Minimax algorithm is to represent the game as a tree structure, where each node represents a possible game state, and the edges represent possible moves by the players. The root of the tree represents the initial game state, and the leaf nodes represent terminal states where the game ends (win, lose, or draw).
Step 2 : Minimax employs a recursive search through the game tree to determine the optimal move for the current player. At each level of the tree, the algorithm alternates between maximizing and minimizing player moves. Max nodes represent the current player’s turn, aiming to maximize their utility (score), while min nodes represent the opponent’s turn, aiming to minimize the current player’s utility.
Step 3 : When the algorithm reaches a leaf node (terminal state) in the game tree, it evaluates the utility of that state using an evaluation function. The evaluation function assigns a numerical value to the terminal state, representing how favorable it is for the current player. The following figure illustrates how the Minimax algorithm (depth = 2) explores the tree step by step :
Step 4 : Once the algorithm has evaluated all possible moves and propagated the scores to the root node, it selects the move corresponding to the highest score at the root level. This chosen move represents the optimal move according to the Minimax algorithm.
Step 5 : To manage computational complexity, Minimax often employs depth-limited search, limiting the depth of the recursive search to a certain level. Depth-limited search ensures that the algorithm explores the game tree to a manageable depth, balancing between computational resources and decision quality.

The pseudocode for the depth-limited Minimax algorithm is presented below.

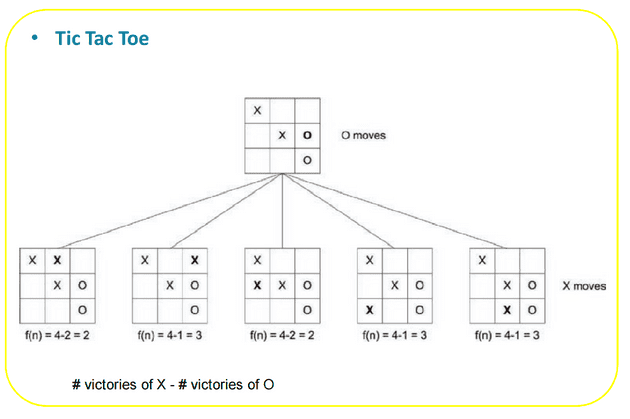
Example for a Static Evaluation in Tic Tac Toe game :

3 - Optimization: Alpha-Beta pruning :

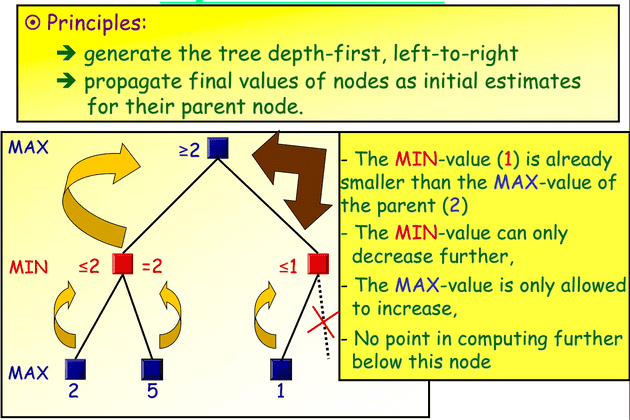
As the game tree expands exponentially, exploring all possible moves becomes computationally expensive and impractical. This is where Alpha-Beta pruning comes into play. Alpha-Beta pruning is an optimization technique used to reduce the number of nodes evaluated by the Minimax algorithm. By intelligently discarding branches of the search tree that are unlikely to lead to a better outcome, Alpha-Beta pruning significantly reduces the search space without affecting the final decision.

Instead of creating the entire tree up to a certain depth and then propagating values, it’s more efficient to interleave the tree generation with value propagation. This means that as nodes are generated and evaluated, their values are immediately propagated up the tree. This approach allows us to identify redundant parts of the tree sooner, as some node values may indicate that further exploration is unnecessary.

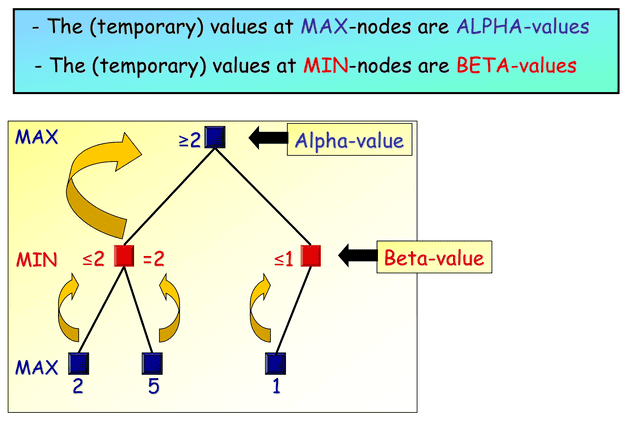
Alpha value represents the best score found so far for the maximizing player, while beta value represents the best score found so far for the minimizing player. These values help limit the search space by indicating when certain branches of the search tree can be pruned, leading to more efficient computation while still finding optimal solutions.

Building a Pente Game with C# using AI with Minimax Algorithm and Alpha Beta Optimization

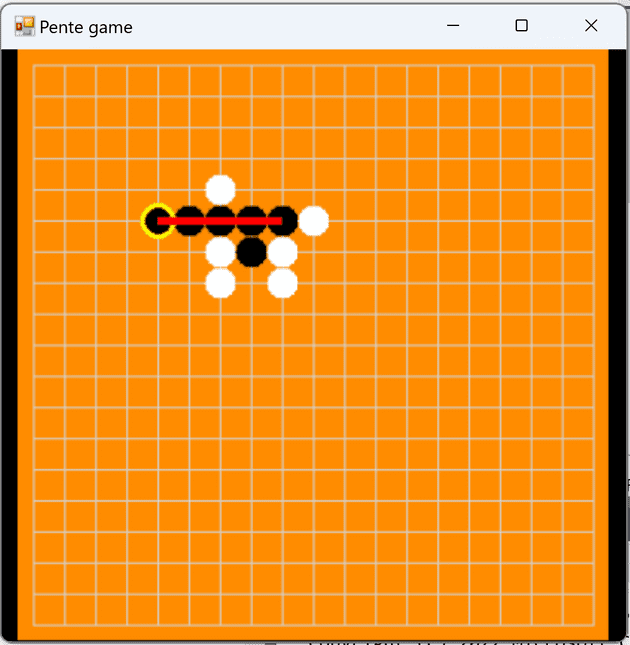
In this part of the project, we will introduce a strategy game called “Pente” (Pente in Greek corresponds to five). This game pits two players against each other: typically White and Black. To win a game, one must align five pieces of their color. The White and Black players take turns placing one of their pieces on the board.

1 - the logic and modelization of the Pente game

To implement the different concepts of the game, we will create the following classes:

1- Place Enumeration : This enumeration allows each position on the board to have a state. That is, whether it is occupied by a black pawn (Black) or a white pawn (White). If the position is not occupied, it will have a value of Null.

internal enum Place
	{
		Null,
		Black,
		White
	}

2- Board Class : This class represents the state of the board at a given moment. The member variables and methods of the Board class are as follows:
- Place[,] area: This is a two-dimensional array that describes the state (Black, White, Null) of all positions on the board.
- int lastMoveX and lastMoveY: These two variables successively contain the X and Y coordinates of the last pawn placed on the board.
- int WhiteCost and BlackCost: These two integers represent the cost of white pawns and the cost of black pawns on the board, respectively. (We will see later in the MiniMax class how we calculate these costs).
- A method IsGameOver: It checks, with each addition of a pawn to the board, if a player has aligned five pawns. If true, it sends a Rectangle object that bounds the aligned pawns, allowing us to draw a line on these pawns. Otherwise, the rectangle is empty, indicating that there are no five aligned pawns on the board.

internal sealed class Board
	{
		public Place[,] area;
		
		public int lastMoveX;

		public int lastMoveY;

		public int _whiteCost;

		public int _blackCost;

		public int WhiteCost
		{
			get
			{
				this._whiteCost = MiniMax.CostBlack(this, Place.White, Place.Black);
				return this._whiteCost;
			}
		}

		public int BlackCost
		{
			get
			{
				this._blackCost = MiniMax.CostBlack(this, Place.Black, Place.White);
				return this._blackCost;
			}
		}

		public Board()
		{
			this.area = new Place[19, 19];
			this.lastMoveX = -1;
			this.lastMoveY = -1;
			this._whiteCost = (this._blackCost = -2147483648);
		}

		public Board(Board origin, int x, int y)
		{
			this.area = (Place[,])origin.area.Clone();
			this.lastMoveX = x;
			this.lastMoveY = y;
			this._whiteCost = (this._blackCost = -2147483648);
		}

		public void init()
		{
			this._whiteCost = (this._blackCost = -2147483648);
		}

		public Rectangle IsGameOver()
		{
			for (int i = 0; i < 19; i++)
			{
				for (int j = 0; j < 19; j++)
				{
					if (this.area[i, j] != Place.Null)
					{
						int num = 1;
						while (num < 5 && j + num < 19 && this.area[i, j] == this.area[i, j + num])
						{
							num++;
						}
						if (num == 5)
						{
							return new Rectangle(i, j, i, j + (num - 1));
						}
						num = 1;
						while (num < 5 && i + num < 19 && this.area[i, j] == this.area[i + num, j])
						{
							num++;
						}
						if (num == 5)
						{
							return new Rectangle(i, j, i + (num - 1), j);
						}
						num = 1;
						while (num < 5 && j + num < 19 && i + num < 19 && this.area[i, j] == this.area[i + num, j + num])
						{
							num++;
						}
						if (num-- == 5)
						{
							return new Rectangle(i, j, i + num, j + num);
						}
						num = 1;
						while (num < 5 && j - num >= 0 && i - num >= 0 && this.area[i, j] == this.area[i - num, j - num])
						{
							num++;
						}
						if (num-- == 5)
						{
							return new Rectangle(i, j, i - num, j - num);
						}
						num = 1;
						while (num < 5 && i + num < 19 && j - num >= 0 && this.area[i, j] == this.area[i + num, j - num])
						{
							num++;
						}
						if (num-- == 5)
						{
							return new Rectangle(i, j, i + num, j - num);
						}
						num = 1;
						while (num < 5 && i - num >= 0 && j + num < 19 && this.area[i, j] == this.area[i - num, j + num])
						{
							num++;
						}
						if (num-- == 5)
						{
							return new Rectangle(i, j, i - num, j + num);
						}
					}
				}
			}
			return Rectangle.Empty;
		}

		public bool IsOver()
		{
			return this.BlackCost >= 100000000 || this.WhiteCost >= 100000000;
		}

		public bool IsNear(int i, int j, int radius)
		{
			for (int k = 0; k <= radius; k++)
			{
				if (i + k < 19 && this.area[i + k, j] != Place.Null)
				{
					return true;
				}
				if (i - k >= 0 && this.area[i - k, j] != Place.Null)
				{
					return true;
				}
				if (j + k < 19 && this.area[i, j + k] != Place.Null)
				{
					return true;
				}
				if (j - k >= 0 && this.area[i, j - k] != Place.Null)
				{
					return true;
				}
				if (j + k < 19 && i + k < 19 && this.area[i + k, j + k] != Place.Null)
				{
					return true;
				}
				if (j - k >= 0 && i + k < 19 && this.area[i + k, j - k] != Place.Null)
				{
					return true;
				}
				if (j + k < 19 && i - k >= 0 && this.area[i - k, j + k] != Place.Null)
				{
					return true;
				}
				if (j - k >= 0 && i - k >= 0 && this.area[i - k, j - k] != Place.Null)
				{
					return true;
				}
			}
			return false;
		}
	}

3- State Enumeration : This enumeration defines the αβ window, where α and β are the two parameters passed to the “Calculate” function in the MiniMax class. Therefore, α represents the best case for the Min player, and β represents the best case for the Max player. In the ideal case, alpha is initialized to -INFINITY and beta to +INFINITY. However, in the case of an “Int” object, α will be initialized to -2147483648 (the smallest value assignable to an integer in C#), while β will have an initial value of 2147483647 (the largest value assignable to an integer in C#). Pruned nodes are those that would be called with a window such that α ≥ β.

internal struct State
	{
		public int alpha;

		public int beta;

		public State(int a, int b)
		{
			this.alpha = a;
			this.beta = b;
		}
	}

4- MiniMax Class : This class implements the MiniMax algorithm. It contains the following member variables and methods:
- A board object of type “Board”: Represents the game board on which the algorithm is applied (the main game board).
- A bestPlay object of type “Board”: Represents the best situation to play, as determined by the MiniMax algorithm.
- WhiteMove() method: Receives the coordinates of the placed pawn and assigns these coordinates to the lastMoveX and lastMoveY variables of the board.
- Calculate() method: This is the most important method, which executes the MiniMax algorithm with Alpha-Beta pruning. It takes the depth parameter and the alpha-beta values as a State object.
- The StateCost() method: Provides a static estimation of a board from the perspective of the Max player (computer). It represents the difference between the cost of a board for black pawns and the cost of a board for white pawns (Static estimation = Black Cost - White Cost). The next point explains how we calculate the cost of a board. We should note that, since the game board has dimensions of 19x19, the maximum depth has been limited to 2 in order to reduce the number of possible cases calculated by the algorithm.
- A Cost() method: Calculates the cost of a board for a given player. It receives 3 parameters:
- An object of type Board: The board for which the cost is calculated.
- An object of type Place (Black or White): The type of player for which the cost is calculated. For example, if the value is Black, the method returns the cost of the board for the Black player.
- An object of type Place (White or Black): The opposite of the previous object. This represents the opponent player.

internal static class MiniMax
	{
		public const int depthDeep = 2;
		public const int size = 19;
		public static Board board;
		public static Board BestPlay;
		private static int[,] horizontalB;
		private static int[,] verticalB;

		private static int[,] diagonal1B;

		private static int[,] diagonal2B;

		private static int[,] verticaliA;

		private static int[,] horizontalA;

		private static int[,] diagonal1A;

		private static int[,] diagonal2A;
		public static void WhiteMove(int x, int y)
		{
			MiniMax.board.lastMoveX = x;
			MiniMax.board.lastMoveY = y;
			MiniMax.board.area[x, y] = Place.White;
		}
		public static void Play()
		{
			DateTime now = DateTime.Now;
			MiniMax.BestPlay = null;
            // alpha = -2147483648
            //beta = + 2147483647
			MiniMax.Calculate(0, new State(-2147483648, 2147483647));
			int num = (int)(DateTime.Now - now).TotalMilliseconds;
			num = 100 - num;
			if (num > 0)
			{
				Thread.Sleep(num);
			}
		}
		private static State Calculate(int depth, State current)
		{
			if (depth < 2 && !MiniMax.board.IsOver())
			{
				for (int i = 0; i < 19; i++)
				{
					for (int j = 0; j < 19; j++)
					{
						if (MiniMax.IsInside(i, j, depth) && MiniMax.board.area[i, j] == Place.Null)
						{
							if (depth % 2 == 0)
							{
								MiniMax.board.area[i, j] = Place.Black;
							}
							else
							{
								MiniMax.board.area[i, j] = Place.White;
							}
							State state = MiniMax.Calculate(depth + 1, current);
							if (depth % 2 == 0)
							{
								if (current.alpha < state.beta)
								{
									current.alpha = state.beta;
									if (depth == 0)
									{
										MiniMax.BestPlay = new Board(MiniMax.board, i, j);
									}
								}
							}
							else if (current.beta > state.alpha)
							{
								current.beta = state.alpha;
							}
							MiniMax.board.area[i, j] = Place.Null;
							if (current.alpha >= current.beta)
							{
								return current;
							}
						}
					}
				}
				for (int k = 0; k < 19; k++)
				{
					for (int l = 0; l < 19; l++)
					{
						if (!MiniMax.IsInside(k, l, depth) && MiniMax.board.area[k, l] == Place.Null)
						{
							if (depth % 2 == 0)
							{
								MiniMax.board.area[k, l] = Place.Black;
							}
							else
							{
								MiniMax.board.area[k, l] = Place.White;
							}
							State state2 = MiniMax.Calculate(depth + 1, current);
							if (depth % 2 == 0)
							{
								if (current.alpha < state2.beta)
								{
									current.alpha = state2.beta;
									if (depth == 0)
									{
										MiniMax.BestPlay = new Board(MiniMax.board, k, l);
									}
								}
							}
							else if (current.beta > state2.alpha)
							{
								current.beta = state2.alpha;
							}
							MiniMax.board.area[k, l] = Place.Null;
							if (current.alpha >= current.beta)
							{
								return current;
							}
						}
					}
				}
			}
			else if (depth % 2 == 0)
			{
				current.alpha = MiniMax.StateCost(MiniMax.board);
			}
			else
			{
				current.beta = MiniMax.StateCost(MiniMax.board);
			}
			return current;
		}
		private static bool IsInside(int i, int j, int depth)
		{
			if (i > 0)
			{
				if (MiniMax.board.area[i - 1, j] != Place.Null)
				{
					return true;
				}
				if (j > 0 && MiniMax.board.area[i - 1, j - 1] != Place.Null)
				{
					return true;
				}
				if (j < 18 && MiniMax.board.area[i - 1, j + 1] != Place.Null)
				{
					return true;
				}
			}
			if (i < 18)
			{
				if (MiniMax.board.area[i + 1, j] != Place.Null)
				{
					return true;
				}
				if (j > 0 && MiniMax.board.area[i + 1, j - 1] != Place.Null)
				{
					return true;
				}
				if (j < 18 && MiniMax.board.area[i + 1, j + 1] != Place.Null)
				{
					return true;
				}
			}
			return (j < 18 && MiniMax.board.area[i, j + 1] != Place.Null) || (j > 0 && MiniMax.board.area[i, j - 1] != Place.Null);
		}
		private static int StateCost(Board current)
		{
			return current.BlackCost - current.WhiteCost;
		}
		public static void NewCost(Board current)
		{
			if (MiniMax.horizontalA == null)
			{
				MiniMax.horizontalB = new int[15, 19];
				MiniMax.verticalB = new int[19, 15];
				MiniMax.diagonal1B = new int[15, 15];
				MiniMax.diagonal2B = new int[15, 15];
				MiniMax.horizontalA = new int[15, 19];
				MiniMax.verticaliA = new int[19, 15];
				MiniMax.diagonal1A = new int[15, 15];
				MiniMax.diagonal2A = new int[15, 15];
			}
			for (int i = 0; i < 19; i++)
			{
				for (int j = 0; j < 19; j++)
				{
					switch (current.area[i, j])
					{
					case Place.Black:
						for (int k = -4; k <= 0; k++)
						{
							MiniMax.Inc(MiniMax.verticalB, i - k, j);
							MiniMax.Inc(MiniMax.horizontalB, i, j - k);
							MiniMax.Inc(MiniMax.diagonal1B, i - k, j - k);
							MiniMax.Inc(MiniMax.diagonal2B, i - k, j + k);
							MiniMax.Block(MiniMax.verticaliA, i - k, j);
							MiniMax.Block(MiniMax.horizontalA, i, j - k);
							MiniMax.Block(MiniMax.diagonal1A, i - k, j - k);
							MiniMax.Block(MiniMax.diagonal2A, i - k, j + k);
						}
						break;
					case Place.White:
						for (int l = -4; l <= 0; l++)
						{
							MiniMax.Block(MiniMax.verticalB, i - l, j);
							MiniMax.Block(MiniMax.horizontalB, i, j - l);
							MiniMax.Block(MiniMax.diagonal1B, i - l, j - l);
							MiniMax.Block(MiniMax.diagonal2B, i - l, j + l);
							MiniMax.Inc(MiniMax.verticaliA, i - l, j);
							MiniMax.Inc(MiniMax.horizontalA, i, j - l);
							MiniMax.Inc(MiniMax.diagonal1A, i - l, j - l);
							MiniMax.Inc(MiniMax.diagonal2A, i - l, j + l);
						}
						break;
					}
				}
			}
			MiniMax.board._blackCost = MiniMax.Count(MiniMax.verticalB) + MiniMax.Count(MiniMax.horizontalB) + MiniMax.Count(MiniMax.diagonal1B) + MiniMax.Count(MiniMax.diagonal2B);
			MiniMax.board._whiteCost = MiniMax.Count(MiniMax.verticaliA) + MiniMax.Count(MiniMax.horizontalA) + MiniMax.Count(MiniMax.diagonal1A) + MiniMax.Count(MiniMax.diagonal2A);
		}
		public static void Inc(int[,] array, int i, int j)
		{
			if (i >= 0 && i < array.GetLength(0) && j >= 0 && j < array.GetLength(1) && array[i, j] != -1)
			{
				array[i, j]++;
			}
		}

		public static void Block(int[,] array, int i, int j)
		{
			if (i >= 0 && i < array.GetLength(0) && j >= 0 && j < array.GetLength(1) && array[i, j] != -1)
			{
				array[i, j] = -1;
			}
		}

		public static int Count(int[,] array)
		{
			int num = 0;
			for (int i = 0; i < array.GetLength(0); i++)
			{
				for (int j = 0; j < array.GetLength(1); j++)
				{
					switch (array[i, j])
					{
					case 1:
						num++;
						break;
					case 2:
						num += 100;
						break;
					case 3:
						num += 10000;
						break;
					case 4:
						num += 1000000;
						break;
					case 5:
						num += 100000000;
						break;
					}
					array[i, j] = 0;
				}
			}
			return num;
		}

		public static int CostBlack(Board current, Place Black, Place White)
		{
			int num = 0;
			for (int i = 0; i < 19; i++)
			{
				int num2 = 0;
				int num3 = 0;
				for (int j = 0; j < 19; j++)
				{
					num3++;
					if (current.area[i, j] == Black)
					{
						num2++;
					}
					else if (current.area[i, j] == White)
					{
						num3 = 0;
						num2 = 0;
					}
					if (num3 == 5)
					{
						num3--;
						switch (num2)
						{
						case 1:
							num++;
							break;
						case 2:
							num += 100;
							break;
						case 3:
							num += 10000;
							break;
						case 4:
							num += 1000000;
							break;
						case 5:
							num += 100000000;
							break;
						}
						if (current.area[i, j - 4] == Black)
						{
							num2--;
						}
					}
				}
			}
			for (int k = 0; k < 19; k++)
			{
				int num4 = 0;
				int num5 = 0;
				for (int l = 0; l < 19; l++)
				{
					num5++;
					if (current.area[l, k] == Black)
					{
						num4++;
					}
					else if (current.area[l, k] == White)
					{
						num5 = 0;
						num4 = 0;
					}
					if (num5 == 5)
					{
						num5--;
						switch (num4)
						{
						case 1:
							num++;
							break;
						case 2:
							num += 100;
							break;
						case 3:
							num += 10000;
							break;
						case 4:
							num += 1000000;
							break;
						case 5:
							num += 100000000;
							break;
						}
						if (current.area[l - 4, k] == Black)
						{
							num4--;
						}
					}
				}
			}
			for (int m = 0; m < 38; m++)
			{
				int num6 = 0;
				int num7 = 0;
				for (int n = 0; n < 19; n++)
				{
					if (m - n < 19 && m - n >= 0)
					{
						num7++;
						if (current.area[m - n, n] == Black)
						{
							num6++;
						}
						else if (current.area[m - n, n] == White)
						{
							num7 = 0;
							num6 = 0;
						}
						if (num7 == 5)
						{
							num7--;
							switch (num6)
							{
							case 1:
								num++;
								break;
							case 2:
								num += 100;
								break;
							case 3:
								num += 10000;
								break;
							case 4:
								num += 1000000;
								break;
							case 5:
								num += 100000000;
								break;
							}
							if (current.area[m - n + 4, n - 4] == Black)
							{
								num6--;
							}
						}
					}
				}
			}
			for (int num8 = -19; num8 < 19; num8++)
			{
				int num9 = 0;
				int num10 = 0;
				for (int num11 = 0; num11 < 19; num11++)
				{
					if (num8 + num11 < 19 && num8 + num11 >= 0)
					{
						num10++;
						if (current.area[num8 + num11, num11] == Black)
						{
							num9++;
						}
						else if (current.area[num8 + num11, num11] == White)
						{
							num10 = 0;
							num9 = 0;
						}
						if (num10 == 5)
						{
							num10--;
							switch (num9)
							{
							case 1:
								num++;
								break;
							case 2:
								num += 100;
								break;
							case 3:
								num += 10000;
								break;
							case 4:
								num += 1000000;
								break;
							case 5:
								num += 100000000;
								break;
							}
							if (current.area[num8 + num11 - 4, num11 - 4] == Black)
							{
								num9--;
							}
						}
					}
				}
			}
			return num;
		}
	}

2 - The calculation of the cost

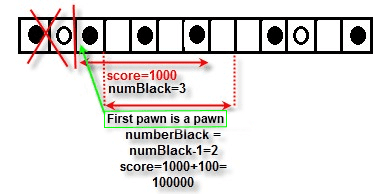
The calculation of the cost is done as follows: (Example for black pawn)

Step 1 : For each row: we calculate the number of possibilities to align 5 black pawns horizontally. To do this, we iterate through the row for 5 iterations with three variables: score (the score obtained in 5 iterations), numBlack (number of black pawns in the 5 iterations), and iterationBlack (number of iterations until 5).
- If a white pawn is found, we start again from the last pawn.
- Else, we continue until reaching 5 iterations, then we test:
  - We decrement iterationBlack to iterate through each pawn.
  - If numBlack=0: the score =10⁰ =1
  - If there is only one black pawn: the score = 10¹ =10
  - If there are 2 black pawns: the score = 10² =100
  - If there are 3 black pawns: the score = 10³=1000
  - If there are 4 black pawns: the score = 10⁴=10000
  - If there are 5 black pawns: the score = 10⁵=100000
  - If the first pawn is black, numBlack- -

Step 2 : For each column: Similarly to the previous method, we calculate the number of possibilities to align 5 black pawns vertically.
Step 3 : An additional improvement would be to calculate the probabilities of aligning 5 pawns diagonally.

Conclusion

In conclusion, exploring the implementation of Minimax with Alpha-Beta pruning in the context of building a Pente game AI has provided valuable insights into the realm of game-playing algorithms. By leveraging these sophisticated techniques, we’ve witnessed the transformation of theoretical concepts into practical solutions, empowering AI agents to make strategic decisions in dynamic and competitive environments. Through the intricate interplay of search algorithms, evaluation functions, and pruning strategies, we’ve not only enhanced our understanding of AI algorithms but also showcased their potential to revolutionize gaming experiences. As we continue to delve deeper into the realm of artificial intelligence, the journey towards creating intelligent game-playing agents serves as a testament to the ingenuity and innovation driving the evolution of AI technology.

You’ve recognized again that the most effective method to enhance and grasp game development is through active game creation.

Best wishes on your AI and game development journey! I wish you all the success ahead!

If you like it, share it!

EL HIRACH ABDERRAZZAK